Importances¶
The Importances plugin provides insights into how individual hyperparameters influence the objective performance of your models. It generates a bar plot displaying the importance scores for each hyperparameter.
This plugin is capable of answering following questions:
Which individual hyperparameters have the greatest impact on the objective performance?
How does the importance of each hyperparameter vary across different budgets?
How does the local parameter importance compare to the global importance as determined by fANOVA?
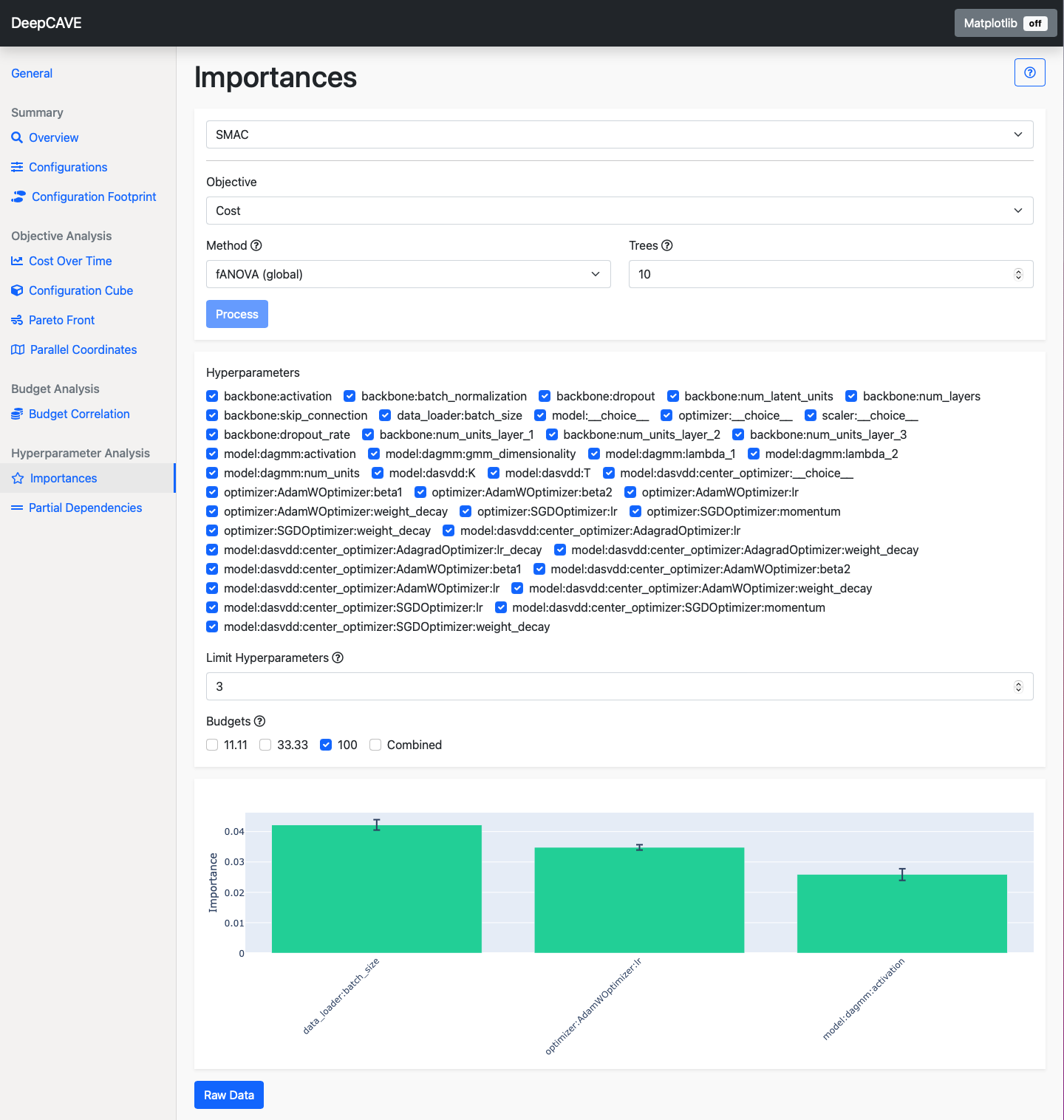
Importance Methods¶
Local Parameter Importance (LPI) focuses on understanding the impact of individual hyperparameters in the context of a specific configuration (here, the incumbent). Leveraging a random forest surrogate model, it calculates the variance in performance caused by changes in each hyperparameter, and expresses this as a fraction of the total variance. This method is especially useful for pinpointing which parameters are crucial in the context of the incumbent their local effects. For more details on LPI, please see the paper CAVE: Configuration Assessment, Visualization and Evaluation.
fANOVA Importance Functional ANOVA (fANOVA) evaluates hyperparameter importance by decomposing the performance variance into contributions from individual hyperparameters and their interactions. It uses a surrogate model, such as a random forest, to predict performance across different hyperparameter configurations, and then analyzes how much each hyperparameter and its interactions contribute to the overall variance in performance. This method provides a comprehensive view of hyperparameter importance across the entire configuration space, thus helping in understanding the global impact of hyperparameters. For more details on fANOVA, please refer to the paper An Efficient Approach for Assessing Hyperparameter Importance.
Multi-Objective Importance¶
Both LPI and fANOVA can be applied to two objectives displaying how the importance changes from one objective to the other. Based on a weighting scheme, the two objectives are scalarized to form a single objective for which the importance is calculated. The resulting plot then shows the scalarized importance for different weightings. The weightings are calculated based on the points on the pareto front which is the set of non-dominated solutions. For more detail on this, please see the paper Hyperparameter Importance Analysis for Multi-Objective AutoML.
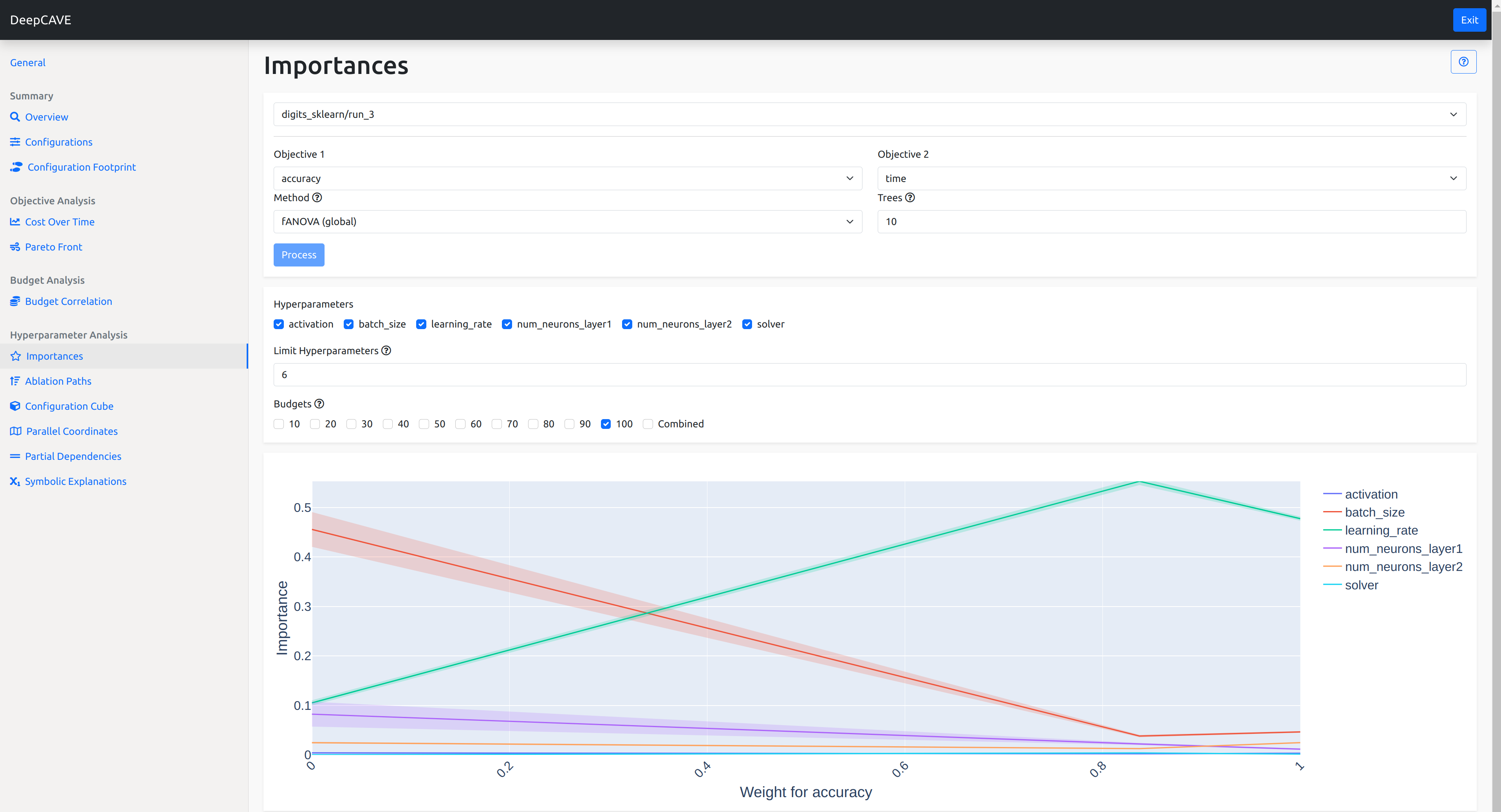
Options¶
Objective 1 / 2: Choose the objective you wish to calculate the importance for. Optionally, choose a second objective to see how the importance changes from one objective to the other.
Method: Whether to calculate the local parameter importance or the fANOVA importance.
Trees: Specify the number of trees for the random forest surrogate model used in calculating importance scores.
To refine your analysis, you can apply various filters after calculation:
Hyperparameters: Display only the importance scores for specific hyperparameters of interest.
Limit Hyperparameters: Show only the top N most important hyperparameters.
Budgets: Filter the results to view importance scores specific to certain multi-fidelity budgets, allowing you to analyze how hyperparameter importance varies with budget changes.
Warning
The fANOVA implementation relies on pyrfr, which cannot be applied to constant hyperparameters. As a workaround, we remove constant hyperparameters before calculation. This will break if the configuration space contains any conditions or forbiddens including constant hyperparameters.