Scalarized Multi-Objective Using ParEGO

This example builds on SVM with Cross-Validation.

Optimize both the final performance and the time used for training.

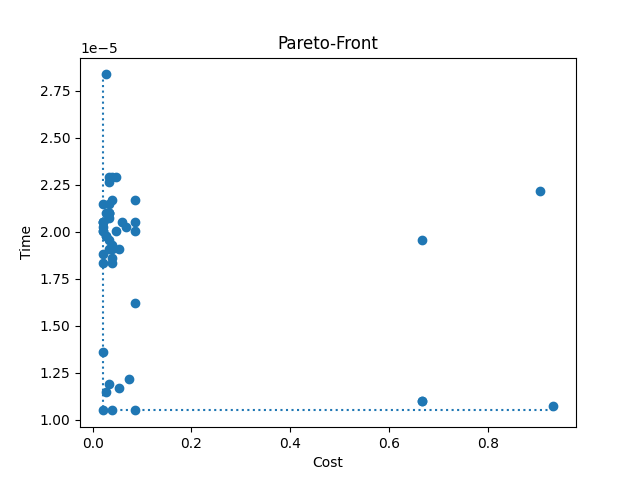
Out:

Default config's cost: 0.033333, training time: 0.000037 seconds
Optimizing! Depending on your machine, this might take a few minutes.

import logging

from smac.multi_objective.parego import ParEGO

logging.basicConfig(level=logging.INFO)

import time

import matplotlib.pyplot as plt
import numpy as np
from ConfigSpace.conditions import InCondition
from ConfigSpace.hyperparameters import (
    CategoricalHyperparameter,
    UniformFloatHyperparameter,
    UniformIntegerHyperparameter,
)
from sklearn import datasets, svm
from sklearn.model_selection import cross_val_score

from smac.configspace import ConfigurationSpace
from smac.facade.smac_hpo_facade import SMAC4HPO
from smac.scenario.scenario import Scenario
from smac.utils.constants import MAXINT

__copyright__ = "Copyright 2021, AutoML.org Freiburg-Hannover"
__license__ = "3-clause BSD"

# We load the iris-dataset (a widely used benchmark)
iris = datasets.load_iris()


def is_pareto_efficient_simple(costs):
    """
    Plot the Pareto Front in our 2d example.

    source from: https://stackoverflow.com/a/40239615
    Find the pareto-efficient points
    :param costs: An (n_points, n_costs) array
    :return: A (n_points, ) boolean array, indicating whether each point is Pareto efficient
    """

    is_efficient = np.ones(costs.shape[0], dtype=bool)
    for i, c in enumerate(costs):
        if is_efficient[i]:
            # Keep any point with a lower cost
            is_efficient[is_efficient] = np.any(costs[is_efficient] < c, axis=1)

            # And keep self
            is_efficient[i] = True
    return is_efficient


def plot_pareto_from_runhistory(observations):
    """
    This is only an example function for 2d plotting, when both objectives
    are to be minimized
    """

    # find the pareto front
    efficient_mask = is_pareto_efficient_simple(observations)
    front = observations[efficient_mask]
    # observations = observations[np.invert(efficient_mask)]

    obs1, obs2 = observations[:, 0], observations[:, 1]
    front = front[front[:, 0].argsort()]

    # add the bounds
    x_upper = np.max(obs1)
    y_upper = np.max(obs2)
    front = np.vstack([[front[0][0], y_upper], front, [x_upper, np.min(front[:, 1])]])

    x_front, y_front = front[:, 0], front[:, 1]

    plt.scatter(obs1, obs2)
    plt.step(x_front, y_front, where="post", linestyle=":")
    plt.title("Pareto-Front")

    plt.xlabel("Cost")
    plt.ylabel("Time")
    plt.show()


def svm_from_cfg(cfg):
    """Creates a SVM based on a configuration and evaluates it on the
    iris-dataset using cross-validation. Note here random seed is fixed.

    It is a multi-objective tae, because we wish to trade-off the time to train
    and the algorithm's final performance.

    Parameters:
    -----------
    cfg: Configuration (ConfigSpace.ConfigurationSpace.Configuration)
        Configuration containing the parameters.
        Configurations are indexable!

    Returns:
    --------
    Dict: A crossvalidated mean score (cost) for the svm on the loaded data-set and the
    second objective; runtime
    """

    # For deactivated parameters, the configuration stores None-values.
    # This is not accepted by the SVM, so we remove them.
    cfg = {k: cfg[k] for k in cfg if cfg[k]}
    # And for gamma, we set it to a fixed value or to "auto" (if used)
    if "gamma" in cfg:
        cfg["gamma"] = cfg["gamma_value"] if cfg["gamma"] == "value" else "auto"
        cfg.pop("gamma_value", None)  # Remove "gamma_value"

    t0 = time.time()
    clf = svm.SVC(**cfg, random_state=42)
    t1 = time.time()

    scores = cross_val_score(clf, iris.data, iris.target, cv=5)
    cost_value = 1 - np.mean(scores)  # Minimize!

    # Return a dictionary with all of the objectives.
    # Alternatively you can return a list in the same order
    # as `multi_objectives`.
    return {"cost": cost_value, "time": t1 - t0}


if __name__ == "__main__":
    # Build Configuration Space which defines all parameters and their ranges
    cs = ConfigurationSpace()

    # We define a few possible types of SVM-kernels and add them as "kernel" to our cs
    kernel = CategoricalHyperparameter(
        name="kernel",
        choices=["linear", "rbf", "poly", "sigmoid"],
        default_value="poly",
    )
    cs.add_hyperparameter(kernel)

    # There are some hyperparameters shared by all kernels
    C = UniformFloatHyperparameter("C", 0.001, 1000.0, default_value=1.0, log=True)
    shrinking = CategoricalHyperparameter("shrinking", [True, False], default_value=True)
    cs.add_hyperparameters([C, shrinking])

    # Others are kernel-specific, so we can add conditions to limit the searchspace
    degree = UniformIntegerHyperparameter("degree", 1, 5, default_value=3)  # Only used by kernel poly
    coef0 = UniformFloatHyperparameter("coef0", 0.0, 10.0, default_value=0.0)  # poly, sigmoid
    cs.add_hyperparameters([degree, coef0])

    use_degree = InCondition(child=degree, parent=kernel, values=["poly"])
    use_coef0 = InCondition(child=coef0, parent=kernel, values=["poly", "sigmoid"])
    cs.add_conditions([use_degree, use_coef0])

    # This also works for parameters that are a mix of categorical and values
    # from a range of numbers
    # For example, gamma can be either "auto" or a fixed float
    gamma = CategoricalHyperparameter("gamma", ["auto", "value"], default_value="auto")  # only rbf, poly, sigmoid
    gamma_value = UniformFloatHyperparameter("gamma_value", 0.0001, 8, default_value=1, log=True)
    cs.add_hyperparameters([gamma, gamma_value])
    # We only activate gamma_value if gamma is set to "value"
    cs.add_condition(InCondition(child=gamma_value, parent=gamma, values=["value"]))
    # And again we can restrict the use of gamma in general to the choice of the kernel
    cs.add_condition(InCondition(child=gamma, parent=kernel, values=["rbf", "poly", "sigmoid"]))

    # Scenario object
    scenario = Scenario(
        {
            "run_obj": "quality",  # we optimize quality (alternatively runtime)
            "runcount-limit": 50,  # max. number of function evaluations
            "cs": cs,  # configuration space
            "deterministic": True,
            "multi_objectives": ["cost", "time"],
            # You can define individual crash costs for each objective
            "cost_for_crash": [1, float(MAXINT)],
        }
    )

    # Example call of the function
    # It returns: Status, Cost, Runtime, Additional Infos
    def_value = svm_from_cfg(cs.get_default_configuration())
    print("Default config's cost: {cost:2f}, training time: {time:2f} seconds".format(**def_value))

    # Optimize, using a SMAC-object
    print("Optimizing! Depending on your machine, this might take a few minutes.")
    # Pass the multi objective algorithm and its hyperparameters
    smac = SMAC4HPO(
        scenario=scenario,
        rng=np.random.RandomState(42),
        tae_runner=svm_from_cfg,
        multi_objective_algorithm=ParEGO,
        multi_objective_kwargs={
            "rho": 0.05,
        },
    )

    incumbent = smac.optimize()

    # pareto front based on smac.runhistory.data
    cost = np.vstack([v[0] for v in smac.runhistory.data.values()])
    plot_pareto_from_runhistory(cost)

previous

MLP with Multi-Fidelity

next

Details