import time
import warnings
import numpy as np
import ConfigSpace
from typing import Dict, Union, List
warnings.filterwarnings('ignore')
Getting started with DEHB¶
DEHB was designed to be an algorithm for Hyper Parameter Optimization (HPO). DEHB uses Differential Evolution (DE) under-the-hood as an Evolutionary Algorithm to power the black-box optimization that HPO problems pose. DE is a black-box optimization algorithm that generates candidate configurations $x$, to the black-box function $f(x)$, that is being optimized. The $x$ is evaluated by the black-box and the corresponding response $y$ is made available to the DE algorithm, which can then use this observation ($x$, $y$), along with previous such observations, to suggest a new candidate $x$ for the next evaluation.
DEHB also uses Hyperband along with DE, to allow for cheaper approximations of the actual evaluations of $x$. Let $f(x)$ be the validation error of training a multilayer perceptron (MLP) on the complete training set. Multi-fidelity algorithms such as Hyperband, allow for cheaper approximations along a possible fidelity. For the MLP, a subset of the dataset maybe a cheaper approximation to the full data set evaluation. Whereas the fidelity can be quantified as the fraction of the dataset used to evaluate the configuration $x$, instead of the full dataset. Such approximations can allow sneak-peek into the black-box, potentially revealing certain landscape features of f(x), thus rendering it a gray-box and not completely opaque and black!
The $z$ parameter is the fidelity parameter to the black-box function. If $z \in [fidelity_{min}, fidelity_{max}]$, then $f(x, fidelity_{max})$ would be equivalent to the black-box case of $f(x)$.
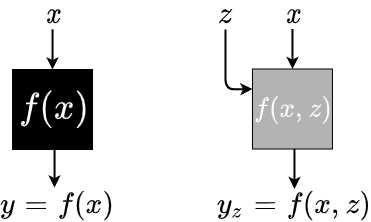
HPO algorithms optimize such black/gray box by wrapping around this target function an interface, by which the algorithms can suggest new $x$ and also consume the result of the corresponding evaluation to store a collection of such ($x$, $y$) pairs. Therefore, to run DEHB, the most essential component required as input is the target function to optimize. Since DEHB can leverage a Hyperband, the target function interface should account for possible input of fidelity too.
Sample interface for target function that DEHB optimizes¶
def target_function(
x: Union[ConfigSpace.Configuration, List, np.array],
fidelity: Union[int, float] = None,
**kwargs
) -> Dict:
""" Target/objective function to optimize
Parameters
----------
x : configuration that DEHB wants to evaluate
fidelity : parameter determining cheaper evaluations
Returns
-------
dict
"""
# ...
# write your code here
# ...
# remove the code snippet below
start = time.time()
y = np.random.uniform() # placeholder response of evaluation
time.sleep(fidelity) # simulates runtime (mostly proportional to fidelity)
cost = time.time() - start
# result dict passed to DE/DEHB as function evaluation output
result = {
"fitness": y, # must-have key that DE/DEHB minimizes
"cost": cost, # must-have key that associates cost/runtime
"info": dict() # optional key containing a dictionary of additional info
}
return result
This target_function is the problem that needs to be solved, or the function to be optimized. The other prerequisite for this function is therefore the domain for its input $x$. In other words, the definition and constraints of the search space for DEHB.
The DE component inside DEHB, assumes that the input domain is scaled to a unit hypercube. This is essential for effective search. If the ConfigSpace library is used to define the domain of $x$, or the parameters of the search space, DEHB can internally handle the scaling to and from the unit hypercube required for search. If ConfigSpace is not used, one needs to additionally handle the scaling of the parameters as an extra interface between DEHB and the target function (or encode it within the target function).
For this template notebook, we will illustrate how a ConfigSpace parameter space can be created.
Defining a sample search space¶
import ConfigSpace
def create_search_space():
# Creating a one-dimensional search space of real numbers in [3, 10]
cs = ConfigSpace.ConfigurationSpace()
cs.add_hyperparameter(ConfigSpace.UniformFloatHyperparameter("x0", lower=3, upper=10, log=False))
return cs
cs = create_search_space()
print(cs)
Configuration space object:
Hyperparameters:
x0, Type: UniformFloat, Range: [3.0, 10.0], Default: 6.5
# Finding dimensionality of search space
dimensions = len(cs.get_hyperparameters())
print(dimensions)
1
# Sampling a random configuration
cs.sample_configuration()
Configuration(values={
'x0': 4.2281773950874,
})
The ConfigSpace documentation can be referred to for more complicated search space creation.
In a similar vein, for a complete gray-box definition, the fidelity domain needs to be defined too. For the earlier example of dataset fractions, the fidelity upper limit cannot clearly exceed 1, and therefore $[0.3, 1]$ is a legitimate definition for such a fidelity. In this template example, we shall simply define the lower and upper range of the fidelity as two parameters that can be input to DEHB. Given that fidelity is being used to simulate cost of runtime in our sample target_function, we shall use a reasonable time range as a placeholder for the fidelity in this case.
Defining fidelity range for the target function¶
min_fidelity, max_fidelity = (0.1, 3)
The above definitions are all the information that DEHB needs about a problem. We are now in a position to call upon DEHB and start running it to tune $x$.
Instantiating and running DEHB¶
from dehb import DEHB
dehb = DEHB(
f=target_function,
dimensions=dimensions,
cs=cs,
min_fidelity=min_fidelity,
max_fidelity=max_fidelity,
output_path="./temp",
n_workers=1 # set to >1 to utilize parallel workers
)
# NOTE: the other hyperparameters to DEHB have been set to certain defaults that were
# empirically determined through related literature, ablation analysis and other experiments,
# but can be tuned as desired
?dehb.run
DEHB allows the option of 3 different resources for its runtime budget:
1) Running DEHB for a certain number of (successive halving) brackets¶
_, _, _ = dehb.run(brackets=1)
print(dehb.vector_to_configspace(dehb.inc_config))
Configuration(values={
'x0': 7.4355666977183,
})
2) Running DEHB for total number of function evaluations¶
# allows optimization to restart from the beginning by forgetting all observations
dehb.reset()
_, _, _ = dehb.run(fevals=20)
print(dehb.get_incumbents())
(Configuration(values={
'x0': 8.3886382525802,
}), 0.1271912991728733)
3) Running DEHB for total amount of wallclock time¶
# allows optimization to restart from the beginning by forgetting all observations
dehb.reset()
_, _, _ = dehb.run(total_cost=10) # run for 10s
print(dehb.get_incumbents())
2024-08-12 11:52:02.652 | WARNING | dehb.optimizers.dehb:_timeout_handler:352 - Runtime budget exhausted. Saving optimization checkpoint now.
(Configuration(values={
'x0': 7.5613710266992,
}), 0.013452343213772533)
Each dehb object initialized maintains a log file in the output_path specified, where the progress and other debugging information is updated. While every alternative DEHB evaluation (and after full optimization), an incumbent.json file is written to disk output_path, with the incumbent (best seen so far) configuration and its corresponding score.
We now rerun DEHB in parallel with 2 workers, and show that the incumbents can be retrieved in any of the following manner:
dehb = DEHB(
f=target_function,
dimensions=dimensions,
cs=cs,
min_fidelity=min_fidelity,
max_fidelity=max_fidelity,
output_path="./temp",
n_workers=2
)
trajectory, runtime, history = dehb.run(
total_cost=20,
)
print(dehb.get_incumbents())
2024-08-12 11:52:05.589 | WARNING | dehb.optimizers.dehb:__init__:264 - A checkpoint already exists, results could potentially be overwritten.
2024-08-12 11:52:25.591 | WARNING | dehb.optimizers.dehb:_timeout_handler:352 - Runtime budget exhausted. Saving optimization checkpoint now.
(Configuration(values={
'x0': 9.6325328773585,
}), 0.007570717149792183)
print(dehb.vector_to_configspace(dehb.inc_config)) # config as ConfigSpace configuration
Configuration(values={
'x0': 9.6325328773585,
})
print(trajectory[-1], dehb.inc_score)
print(dehb.vector_to_configspace(dehb.inc_config))
0.007570717149792183 0.007570717149792183
Configuration(values={
'x0': 9.6325328773585,
})
Conclusion¶
As detailed above, the problem definition needs to be input to DEHB as the following information:
- the target_function (
f) that is the primary black-box function to optimize, - the fidelity range of
min_fidelityandmax_fidelitythat allows the cheaper, faster gray-box optimization offand - the search space or the input domain of the function
f, that can be represented as aConfigSpaceobject and passed to DEHB at initialization.
Following which, DEHB can be run for any amount of practical real-world budget. It can be run for either:
- a total amount of actual wallclock time, example one day (~86400 seconds), or
- a total number of function evaluations, or the number of times we want the black-box to be accessed for evaluation, across all fidelities or
- the total number of brackets we want to run the DEHB algorithm for.
DEHB will terminate once its chosen runtime budget is exhausted, and report the incumbent found. DEHB, as an anytime algorithm, constantly writes to disk a lightweight json file with the best found configuration and its score seen till that point.